对于学生来说寒假是很好的迎头赶上,查漏补缺的机会!寒假利用得当将会为不久的高考积攒下一笔财富。但怎样复习有的学生可能会感觉到迷茫,高考主要从“基础、方法、综合、创新“这几个方面考查,那么我们也主要从这几个方面入手逐步进行复习巩固提高,北京四中网校教学高中部杨老师给同学们一些学习指导,希望对同学们有所帮助。
一、 巩固基础,润物无声
“基础不牢,地动山摇”一切技能的掌握,训练基本功都是一门必修课。数学学习更是如此。只有很好的掌握了公式、定理这些最基础的东西才能在方法、能力上有所突破。因此在寒假里首先要掌握每个知识模块中的基本公式和基本定理,做到烂熟于心,因为高考中很多考题用基本公式就能解答。下面我们看一道高考题。 例1.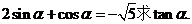 这是一道高考题,原题为选择题。就是这么一道以基础立意的简单题,很多学生却在这道题上栽了跟头。原因就是基础不牢,信心不足,结果导致半途而废,遗憾收场。本题利用同角三角函数公式 这是一道高考题,原题为选择题。就是这么一道以基础立意的简单题,很多学生却在这道题上栽了跟头。原因就是基础不牢,信心不足,结果导致半途而废,遗憾收场。本题利用同角三角函数公式![]() 和题中条件联立即可作答。解析: 和题中条件联立即可作答。解析:
第一步: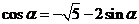 ① ①
第二步:将①式代入![]() 化简整理可得 化简整理可得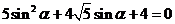 ② ②
很多同学做到了第二步,离成功已很近了,但是感觉到方程有点繁琐,就放弃了解答,这就是信心不足造成的。 这里我们只需利 用求根公式就很容易得到: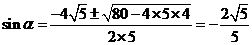 ③ ③
将③式代入 ①式可得: 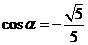 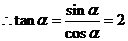
本题做不出来的原因,就是基础掌握不牢,缺乏自信造成的。因此在复习中要首先掌握好基础,“随风潜入夜,润物细无声”在掌握好基础的同时,也在潜移默化中学到了技能和方法。
二、 总结方法,有的放矢 “工欲善其事,必先利其器”,有一个好的方法,我们在做题的过程中就可以收到事半功倍的效果。在基础掌握牢固的基础上接下来就要总结解决每个类型题所要用到的方法。解决一类题,都有一个固定的套路。这些方法和套路,老师在课堂上都有总结。比如对于三角函数解答题我们都要利用降幂公式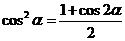 , ,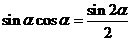 和辅助角公式 和辅助角公式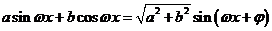 转化为 转化为 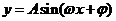 进行研究。对于例1来说如果我们采用这种方法就会简单很多。 进行研究。对于例1来说如果我们采用这种方法就会简单很多。
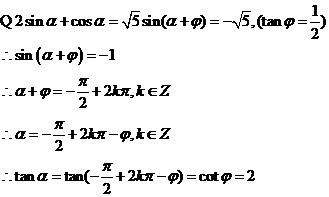
另外,数列模块如何求通项公式以及如何求数列的前n项和,这些都有具体的方法,掌握这些方法,在解题中往里面套就可以了。此外概率统计和立体几何问题也有其对应的具体方法,只要善于总结,在解题中就能做到,有的放矢,游刃有余。
三、 提升能力, 更上层楼
高考除了考查基础知识和基本能力外,还要对考生的综合能力进行考查。也就是考查知识的迁移能力,就是利用新方法解决老问题或者利用老方法解决新问题。最简单的例子,学习向量时,我们利用向量知识,解决单纯的向量问题。在很好的掌握了向量之后,还可以利用向量知识,解决几何中的有关平行,垂直,夹角和距离问题。再如导数的实质是变化率问题,我们也可以利用导数求函数的单调区间和曲线的切线方程。
譬如上面的例1我们利用三角函数知识解决,略显麻烦。如果我们抓住了本质,利用导数解决就很非常快捷,下面我给出解析
解析:构造函数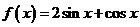 ,显然f(x)的最值是 ,显然f(x)的最值是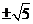
此法简单,快捷,省时,省力。只要我们平时勤于思考,善于联系,就能在学习中更上一层楼!
四、 学会创新,推陈出新
此外,高考还考查创新能力。初中数学的学习是模仿和练习,高中数学的学习是联想和转化,同时也要求考生具有一定的创新能力。创新能力的培养需要我们在平时训练中善于联想和转化,通过联想和不断转化产生新思路发现新方法。
例2.已知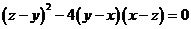 ,求证: ,求证: 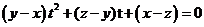
分析:本题短小精巧,看似简单,却又难以下手,如果上来就将条件中的式子展开,就会陷入麻烦。此时我们就要仔细观察,联想和联系。观察式子结构发现它很像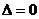 ,这又与一元二次方程有关,于是构造一元二次方程,本题就迎刃而解。 ,这又与一元二次方程有关,于是构造一元二次方程,本题就迎刃而解。
解析:构造一元二次方程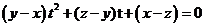 因为y-x+z-y+x-z=0所以t=1为方程的根.又因 因为y-x+z-y+x-z=0所以t=1为方程的根.又因![]() 所以方程又两个相等的实数根1. 由根与系数的关系可得: 所以方程又两个相等的实数根1. 由根与系数的关系可得: ![]() ,所以 ,所以 ![]()
本题通过联想通过构造一元二次方程,大大简化了解题步骤,优化了解题思路。
数学是思维的体操,数学问题互相联系.一题多解、多题一解,转变观察问题的角度,它必然成为培养创新能力,养成创新意识的主要渠道。还在为学习迷茫的你,快快行动吧! |